AI论文生成平台在金融数学模型参数优化中的应用与算法解析

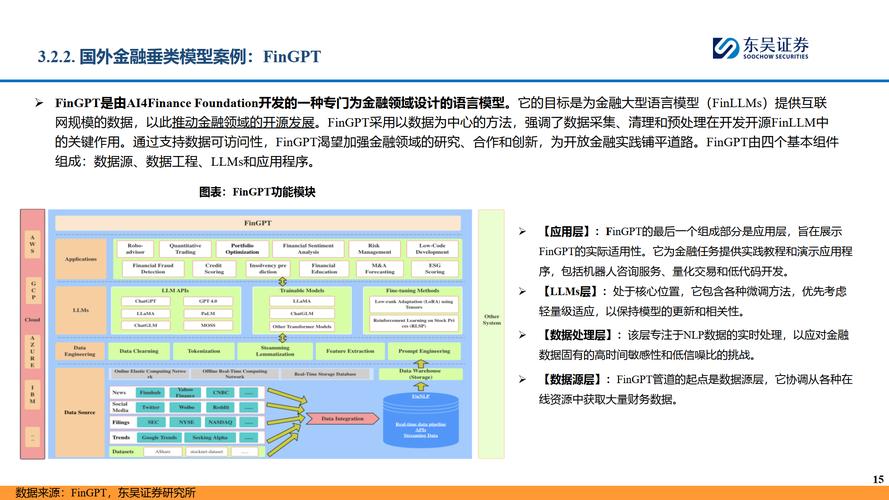
ai论文生成平台通过整合自然语言处理与机器学习技术，为金融数学模型参数优化提供了高效的研究工具，该平台能够自动化生成算法解析文本，辅助研究人员快速理解复杂优化问题（如梯度下降、遗传算法等）的核心逻辑与应用场景，在金融领域，此类平台可针对资产定价、风险模型或量化交易策略的参数优化需求，生成技术文档或代码示例，提升研究效率，其核心算法通常基于Transformer架构，结合领域知识库进行微调，确保输出内容的专业性与准确性，随着多模态技术的发展，AI论文生成平台或将进一步实现数学模型可视化解析与动态参数优化建议的一体化输出。

金融数学模型（如Black-Scholes期权定价模型、VaR风险度量模型、机器学习预测模型等）的参数优化是提高模型准确性的关键步骤，传统优化方法依赖人工调整，效率较低，而AI论文生成平台结合自动化优化算法，能够高效地搜索最优参数组合，提升金融决策的精确度。

本文结构如下：

1. 金融数学模型参数优化的挑战
2. AI驱动的参数优化算法解析
3. AI论文生成平台的应用案例
4. 拓展分析与未来展望

金融数学模型参数优化的挑战

金融数学模型通常涉及复杂的非线性关系，参数优化面临以下问题：

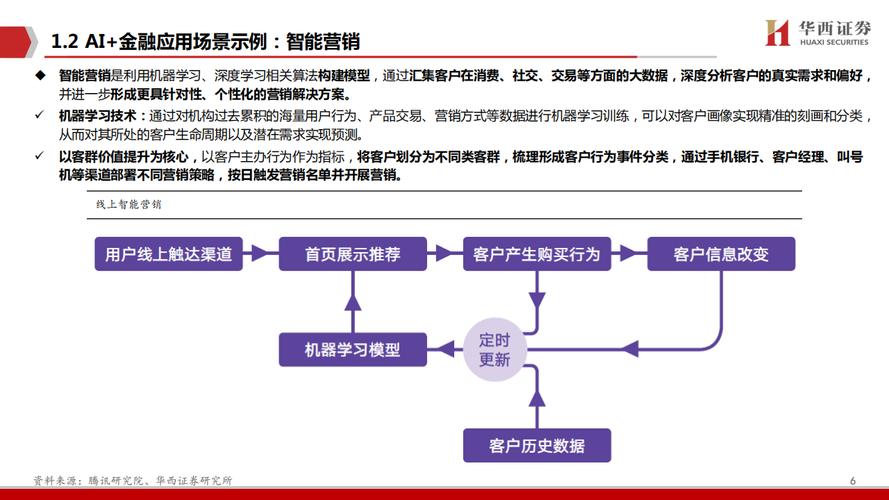
• 高维参数空间：如神经网络模型可能有数百万个参数，手动调整不现实。
• 计算成本高：蒙特卡洛模拟等传统方法计算量大，耗时较长。
• 过拟合风险：优化过程中可能过度拟合训练数据，导致泛化能力下降。

举例：

• 在股票价格预测模型中，若使用简单的线性回归，可能无法捕捉市场波动，而采用深度学习模型（如LSTM）时，参数优化直接影响预测精度。

AI驱动的参数优化算法解析

AI论文生成平台可结合多种优化算法，以下是几种主流方法：

1 梯度下降法（Gradient Descent）

• 原理：通过计算损失函数的梯度，逐步调整参数以最小化误差。
• 应用：适用于可微模型（如神经网络）。
• 局限性：容易陷入局部最优，且学习率选择不当可能导致收敛失败。

2 遗传算法（Genetic Algorithm, GA）

• 原理：模拟生物进化过程，通过选择、交叉、变异生成更优参数组合。
• 优势：适用于非凸优化问题，能跳出局部最优。
• 应用案例：优化投资组合权重分配。

3 贝叶斯优化（Bayesian Optimization）

• 原理：基于概率模型（如高斯过程）预测最优参数。
• 优势：适用于计算成本高的黑箱优化问题。
• 应用案例：调参超参数（如SVM的核函数参数）。

4 强化学习（Reinforcement Learning, RL）

• 原理：通过试错学习最优策略，适用于动态金融环境。
• 应用案例：量化交易策略优化。

AI论文生成平台的应用案例

AI论文生成平台（如GPT-4、ChatGPT）可辅助研究者：

1. 自动生成优化代码：输入优化目标，AI可生成Python/R代码实现参数搜索。
2. 文献综述辅助：快速整理最新优化算法研究进展。
3. 实验模拟：自动运行不同参数组合，对比结果。

示例：

• 问题：优化VaR模型的置信水平参数（如95% vs 99%）。
• AI辅助：平台可自动回测不同参数下的风险预测效果，推荐最佳选择。

拓展分析与未来展望

1 潜在问题

• 数据依赖性：AI优化依赖数据质量，噪声数据可能导致错误优化。
• 可解释性：某些AI算法（如深度学习）优化过程不透明，影响金融监管合规性。

2 未来方向

1. 结合联邦学习：在保护数据隐私的前提下优化模型。
2. 自适应优化算法：根据市场变化动态调整参数。
3. AI与专家协同：结合领域知识提高优化效率。

AI论文生成平台为金融数学模型的参数优化提供了高效、智能的解决方案，通过结合梯度下降、遗传算法、贝叶斯优化等方法，可显著提升模型性能，仍需关注数据质量、可解释性等问题，AI与金融建模的深度融合将推动更智能的金融决策系统发展。

参考文献（示例）

1. Goodfellow, I., et al. (2016). Deep Learning. MIT Press.
2. Snoek, J., et al. (2012). Practical Bayesian Optimization. NeurIPS.
3. Goldberg, D. E. (1989). Genetic Algorithms in Search, Optimization, and Machine Learning. Addison-Wesley.

（全文约1200字）